Table of Contents
Misure in decibel
Il decibel (simbolo dB) è la decima parte del bel (simbolo B): 10 dB = 1 B ed è un'unità di misura logaritmica del rapporto fra due grandezze omogenee (di potenza). Vedi la voce su Wikipedia.
Fissata una potenza di riferimento p0, è possibile calcolare il rapporto in decibel con un'altra potenza p1 espressa nella stessa unità di misura usando questa formula:
dB (power ratio) = 10·log(p1/p0)
Guadagno o attenuazione di potenza
Secondo la definizione i decibel sono usati per misurare il rapporto fra due potenze (ad esempio espresse in watt), pertanto la misura risulta un numero puro, senza unità di misura.
Attenuazione di potenza
Fatta 100 la potenza p0 di riferimento, ecco una tabella di attenuazione in dB per le relative potenze p1:
| p1 | p0 | Rapporto | dB |
|---|---|---|---|
| 100 | 100 | 10·log(100/100) | 0.00 |
| 90 | 100 | 10·log(90/100) | -0.46 |
| 80 | 100 | 10·log(80/100) | -0.97 |
| 70 | 100 | 10·log(70/100) | -1.55 |
| 60 | 100 | 10·log(60/100) | -2.22 |
| 50 | 100 | 10·log(50/100) | -3.01 |
| 40 | 100 | 10·log(40/100) | -3.98 |
| 30 | 100 | 10·log(30/100) | -5.23 |
| 20 | 100 | 10·log(20/100) | -6.99 |
| 10 | 100 | 10·log(10/100) | -10.00 |
Quindi dimezzare una potenza significa applicare una attenuazione di circa -3 dB, ridurre la potenza a un decimo equivale ad una attenuazione di -10 db.
Guadagno di potenza
Fatta 100 la potenza p0 di riferimento, ecco una tabella di guadagno in dB per le relative potenze p1:
| p1 | p0 | Rapporto | dB |
|---|---|---|---|
| 100 | 100 | 10·log(100/100) | 0.00 |
| 120 | 100 | 10·log(120/100) | 0.79 |
| 140 | 100 | 10·log(140/100) | 1.46 |
| 160 | 100 | 10·log(160/100) | 2.04 |
| 180 | 100 | 10·log(180/100) | 2.55 |
| 200 | 100 | 10·log(200/100) | 3.01 |
| 400 | 100 | 10·log(400/100) | 6.02 |
| 600 | 100 | 10·log(600/100) | 7.78 |
| 800 | 100 | 10·log(800/100) | 9.03 |
| 1000 | 100 | 10·log(1000/100) | 10.00 |
Quindi raddoppiare una potenza significa applicare un guadagno di circa 3 dB, aumentare la potenza di dieci volte equivale ad un guadagno di 10 db.
Usare i volt invece dei watt
In elettronica spesso si preferisce utilizzare i volt invece dei watt. Cioè, dato un circuito con una impedenza prefissata, si vuole conoscere l'attenuazione o il guadagno (in decibel) che si ottiene alla variazione della tensione (cioè al rapporto fra due tensioni) perché la grandezza che possiamo controllare è la tensione, non la potenza.
Questa la legge che lega la potenza alla tensione:
Potenza (Watt) = Tensione (Volt) x Intensità (Ampere)
La legge di Ohm dice come ricavare l'intensità di corrente dalla tensione e dalla resistenza:
Intensità (Ampere) = Tensione (Volt) / Resistenza (Ohm)
Quindi la potenza può essere calcolata con:
Potenza (Watt) = Tensione (Volt) ^2 / Resistenza (Ohm)
In definitiva, facendo il rapporto fra le due potenze espresse in v^2/Ω, si ha che la resistenza scompare (perché è costante ed è presente sia al numeratore che al denominatore) e resta solo il rapporto del quadrato della tensione. Grazie alle proprietà dei logaritmi si ottiene la formula dei decibel:
dB (power ratio) = 10·log(p1/p0) = 10·log(v1^2/v0^2) = 20·log(v1/v0)
Attenuazione di tensione
Fatta 100 la tensione v0 di riferimento, ecco una tabella di attenuazione in dB per le relative tensioni v1:
| v1 | v0 | Rapporto | dB |
|---|---|---|---|
| 100 | 100 | 20·log(100/100) | 0.00 |
| 90 | 100 | 20·log(90/100) | -0.92 |
| 80 | 100 | 20·log(80/100) | -1.94 |
| 70 | 100 | 20·log(70/100) | -3.10 |
| 60 | 100 | 20·log(60/100) | -4.44 |
| 50 | 100 | 20·log(50/100) | -6.02 |
| 40 | 100 | 20·log(40/100) | -7.96 |
| 30 | 100 | 20·log(30/100) | -10.46 |
| 20 | 100 | 20·log(20/100) | -13.98 |
| 10 | 100 | 20·log(10/100) | -20.00 |
Quindi dimezzare una tensione significa ottenere una attenuazione di circa -6 dB. Ridurre la tensione a un decimo equivale ad una attenuazione di -20 db, che in termini di potenza è una riduzione a un centesimo.
Ad esempio uno strumento VU Meter misura il volume di un segnale sonoro (Volume Unit) in rapporto ad un segnale di riferimento considerato il massimo gestibile senza distorsioni. La lettura è espressa in decibel rispetto alla tensione in volt.
Guadagno di tensione
Fatta 100 la tensione v0 di riferimento, ecco una tabella di guadagno in dB per le relative tensioni v1:
| v1 | v0 | Rapporto | dB |
|---|---|---|---|
| 100 | 100 | 20·log(100/100) | 0.00 |
| 125 | 100 | 20·log(125/100) | 1.94 |
| 150 | 100 | 20·log(150/100) | 3.52 |
| 175 | 100 | 20·log(175/100) | 4.86 |
| 200 | 100 | 20·log(200/100) | 6.02 |
| 300 | 100 | 20·log(300/100) | 9.54 |
| 400 | 100 | 20·log(400/100) | 12.04 |
| 600 | 100 | 20·log(600/100) | 15.56 |
| 800 | 100 | 20·log(800/100) | 18.06 |
| 1000 | 100 | 20·log(1000/100) | 20.00 |
Quindi raddoppiare la tensione significa ottenere un guadagno di circa 6 dB. Aumentare la tensione di dieci volte equivale ad un guadagno di 20 db, che in termini di potenza è una aumento di cento volte.
Segnale digitale
Quando si trasforma un segnale audio analogico in digitale generalmente si utilizza una misura proporzionale alla tensione (non alla potenza) e il massimo livello digitale dipende dai bit utilizzati per ogni campione.
In questo caso in genere le misure di attenuazione o guadagno sono espresse in dBFS (decibels relative to full scale), per cui il valore di riferimento pari a 0 dBFS corrisponde ad un segnale che arriva a fondo scala (massimo valore del segnale digitale). Una attenuazione di -6 dBFS corrisponde ad un segnale pari al 50% del massimo, -20 dBFS equivalgono ad un segnale pari al 10% del fondo scala (cioè 1/100 della potenza massima), ecc.
Applicare un guadagno (cioè un valore dBFS superiore allo zero) ad un segnale digitale può comportare il rischio di clipping, cioè quando il valore risultante va oltre il fondo scala consentito dai bit di campionamento disponibili.
Misura del rumore
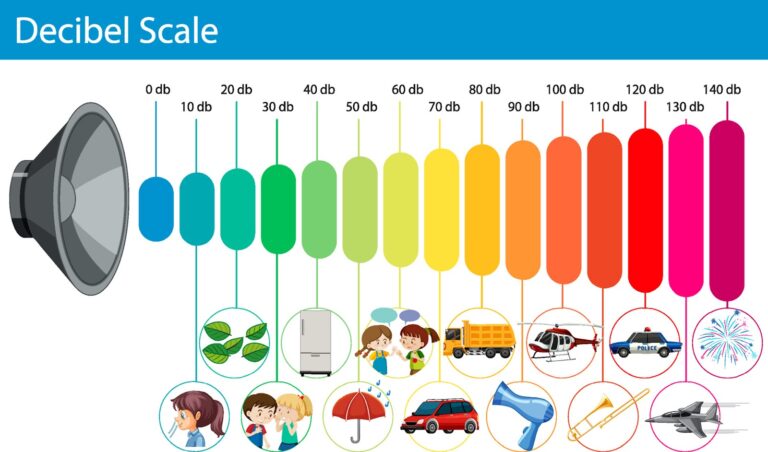
Quando si vuole misurare il livello di rumore percepito da una persona, la potenza sonora di riferimento è il rumore minimo che l'orecchio umano riesce a percepire; a questo viene assegnato il livello di 0 dB (0 dB Hearing Level).
In questo caso si parla di propriamente di potenza sonora, quindi la formula dei decibel è quella con fattore 10.
- Quasi silenzio: 0 dB (10xlog(1) = 0)
- Un souno 10 volte più potente: 10 dB (10xlog(10) = 10)
- Un souno 100 volte più potente del quasi silenzio: 20 dB (10xlog(100) = 20)
- Un souno 1000 volte più potente del quasi silenzio: 30 dB (10xlog(1000) = 30)
Pressione sonora di un rumore
Si possono usare diversi strumenti - ad esempio dei microfoni - per misurare la pressione acustica o sonora di un suono (cioè l'ampiezza dell'onda sonora che varia nel tempo). Tale grandezza è proporzionale alla radice quadrata della potenza del suono stesso. Pertanto, quando si esprime un guadagno o una attenuazione in decibel rispetto ad un rumore di riferimento, si deve usare la formula logaritmica con coefficiente moltiplicatore 20 (analogamente a quando si misura la tensione invece della potenza in elettrotecnica).
Il livello di pressione sonora (SPL) è una misura del valore efficace dell'onda meccanica; data una pressione acustica di riferimento ps0, il livello di una pressione acustica ps1 si esprime in dB(SPL) ed è dato dalla formula:
dB(SPL) = 20 x log(ps1/ps0)
Ecco alcuni esempi di valori in decibel SPL, per suoni o rumori registrati ad 1 m di distanza:
- Silenzio quasi totale: 0 dB
- Sussurro: 15 dB
- Normale conversazione: 60 dB
- Tosaerba: 90 dB
- Clacson di auto: 110 dB
- Concerto rock o motore di jet: 120 dB
- Sparo o fuochi artificali: 140 dB