Virtual Earth Tile System (V4)
Other (free) doc: OpenLayers. Layer. SphericalMercator.
From microsoft.com
Virtual Earth (aka Windows Live Local) provides a world map that users can directly manipulate to pan and zoom. To make this interaction as fast and responsive as possible, we chose to pre-render the map at many different levels of detail, and to cut each map into tiles for quick retrieval and display. This document describes the projection, coordinate systems, and addressing scheme of the map tiles, which collectively are called the Virtual Earth Tile System.
Map Projection
To make the map seamless, and to ensure that aerial images from different sources line up properly, we have to use a single projection for the entire world. We chose to use the Mercator projection, which looks like this:
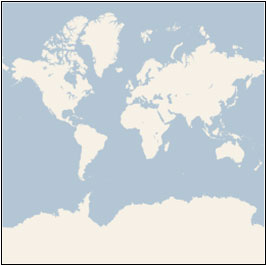
Although the Mercator projection significantly distorts scale and area (particularly near the poles), it has two important properties that outweigh the scale distortion:
It’s a conformal projection, which means that it preserves the shape of relatively small objects. This is especially important when showing aerial imagery, because we want to avoid distorting the shape of buildings. Square buildings should appear square, not rectangular.
It’s a cylindrical projection, which means that north and south are always straight up and down, and west and east are always straight left and right.
Since the Mercator projection goes to infinity at the poles, it doesn’t actually show the entire world. Using a square aspect ratio for the map, the maximum latitude shown is approximately 85.05 degrees.
To simplify the calculations, we use the spherical form of this projection, not the ellipsoidal form. Since the projection is used only for map display, and not for displaying numeric coordinates, we don’t need the extra precision of an ellipsoidal projection. The spherical projection causes approximately 0.33% scale distortion in the Y direction, which is not visually noticeable.
Ground Resolution and Map Scale
In addition to the projection, the ground resolution or map scale must be specified in order to render a map. At the lowest level of detail (Level 1), the map is 512 x 512 pixels. At each successive level of detail, the map width and height grow by a factor of 2: Level 2 is 1024 x 1024 pixels, Level 3 is 2048 x 2048 pixels, Level 4 is 4096 x 4096 pixels, and so on. In general, the width and height of the map (in pixels) can be calculated as:
map width = map height = 256 * (2 ^ level) pixels
The ground resolution indicates the distance on the ground that’s represented by a single pixel in the map. For example, at a ground resolution of 10 meters/pixel, each pixel represents a ground distance of 10 meters. The ground resolution varies depending on the level of detail and the latitude at which it’s measured. Using an earth radius of 6378137 meters, the ground resolution (in meters per pixel) can be calculated as:
ground resolution = cos(latitude * pi/180) * earth circumference / map width
= (cos(latitude * pi/180) * 2 * pi * 6378137 meters) / (256 * (2 ^ level) pixels)
The map scale indicates the ratio between map distance and ground distance, when measured in the same units. For instance, at a map scale of 1 : 100,000, each inch on the map represents a ground distance of 100,000 inches. Like the ground resolution, the map scale varies with the level of detail and the latitude of measurement. It can be calculated from the ground resolution as follows, given the screen resolution in dots per inch, typically 96 dpi:
map scale = 1 : ground resolution * screen dpi / 0.0254 meters/inch
= 1 : (cos(latitude * pi/180) * 2 * pi * 6378137 * screen dpi) / (256 * (2 ^ level) * 0.0254)
This table shows each of these values at each level of detail, as measured at the Equator. (Note that the ground resolution and map scale also vary with the latitude, as shown in the equations above, but not shown in the table below.)
| Level of Detail | Map Width and Height (pixels) | Ground Resolution (meters / pixel) | Map Scale(at 96 dpi) |
| 1 | 512 | 78,271.5170 | 1 : 295,829,355.45 |
| 2 | 1,024 | 39,135.7585 | 1 : 147,914,677.73 |
| 3 | 2,048 | 19,567.8792 | 1 : 73,957,338.86 |
| 4 | 4,096 | 9,783.9396 | 1 : 36,978,669.43 |
| 5 | 8,192 | 4,891.9698 | 1 : 18,489,334.72 |
| 6 | 16,384 | 2,445.9849 | 1 : 9,244,667.36 |
| 7 | 32,768 | 1,222.9925 | 1 : 4,622,333.68 |
| 8 | 65,536 | 611.4962 | 1 : 2,311,166.84 |
| 9 | 131,072 | 305.7481 | 1 : 1,155,583.42 |
| 10 | 262,144 | 152.8741 | 1 : 577,791.71 |
| 11 | 524,288 | 76.4370 | 1 : 288,895.85 |
| 12 | 1,048,576 | 38.2185 | 1 : 144,447.93 |
| 13 | 2,097,152 | 19.1093 | 1 : 72,223.96 |
| 14 | 4,194,304 | 9.5546 | 1 : 36,111.98 |
| 15 | 8,388,608 | 4.7773 | 1 : 18,055.99 |
| 16 | 16,777,216 | 2.3887 | 1 : 9,028.00 |
| 17 | 33,554,432 | 1.1943 | 1 : 4,514.00 |
| 18 | 67,108,864 | 0.5972 | 1 : 2,257.00 |
| 19 | 134,217,728 | 0.2986 | 1 : 1,128.50 |
| 20 | 268,435,456 | 0.1493 | 1 : 564.25 |
| 21 | 536,870,912 | 0.0746 | 1 : 282.12 |
| 22 | 1,073,741,824 | 0.0373 | 1 : 141.06 |
| 23 | 2,147,483,648 | 0.0187 | 1 : 70.53 |
Pixel Coordinates
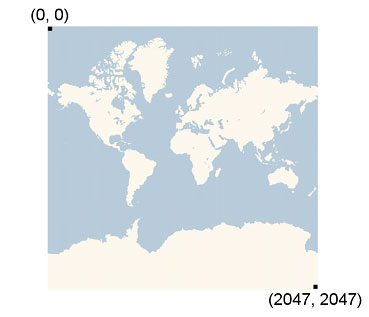
Having chosen the projection and scale to use at each level of detail, we can convert geographic coordinates into pixel coordinates. Since the map width and height is different at each level, so are the pixel coordinates. The pixel at the upper-left corner of the map always has pixel coordinates (0, 0). The pixel at the lower-right corner of the map has pixel coordinates (width-1, height-1), or referring to the equations in the previous section, (256 * (2 ^ level) – 1, 256 * (2 ^ level) – 1). For example, at level 3, the pixel coordinates range from (0, 0) to (2047, 2047), like this:
Given latitude and longitude in degrees, and the level of detail, the pixel XY coordinates can be calculated as follows:
sinLatitude = sin(latitude * pi/180)
pixelX = ((longitude + 180) / 360) * 256 * (2 ^ level)
pixelY = (0.5 – log((1 + sinLatitude) / (1 – sinLatitude)) / (4 * pi)) * 256 * (2 ^ level)
The latitude and longitude are assumed to be on the WGS 84 datum. Even though Virtual Earth uses a spherical projection, it’s important to convert all geographic coordinates into a common datum, and WGS 84 was chosen to be that datum. The longitude is assumed to range from -180 to +180 degrees, and the latitude must be clipped to range from -85.05112878 to 85.05112878. This avoids a singularity at the poles, and it causes the projected map to be square.
Tile Coordinates and Quadkeys
To optimize the performance of map retrieval and display, the rendered map is cut into tiles of 256 x 256 pixels each. As the number of pixels differs at each level of detail, so does the number of tiles:
map width = map height = (2 ^ level) tiles
Each tile is given XY coordinates ranging from (0, 0) in the upper left to 1)
 Given a pair of pixel XY coordinates, you can easily determine the tile XY coordinates of the tile containing that pixel:
Given a pair of pixel XY coordinates, you can easily determine the tile XY coordinates of the tile containing that pixel:
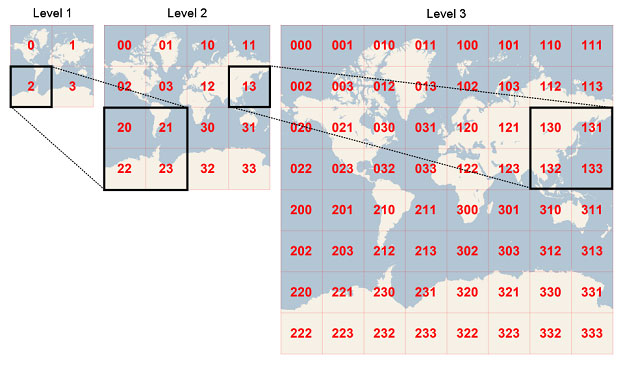 Finally, quadkeys provide a one-dimensional index key that usually preserves the proximity of tiles in XY space. In other words, two tiles that have nearby XY coordinates usually have quadkeys that are relatively close together. This is important for optimizing database performance, because neighboring tiles are usually requested in groups, and it’s desirable to keep those tiles on the same disk blocks, in order to minimize the number of disk reads.
===== Sample Code =====
The following sample C# code illustrates how to implement the functions described in this document. These functions can be easily translated into other programming languages as needed.
Finally, quadkeys provide a one-dimensional index key that usually preserves the proximity of tiles in XY space. In other words, two tiles that have nearby XY coordinates usually have quadkeys that are relatively close together. This is important for optimizing database performance, because neighboring tiles are usually requested in groups, and it’s desirable to keep those tiles on the same disk blocks, in order to minimize the number of disk reads.
===== Sample Code =====
The following sample C# code illustrates how to implement the functions described in this document. These functions can be easily translated into other programming languages as needed.

